Level Order Unary Degree Sequence (LOUDS)
Level Order Unary Degree Sequence or LOUDS is a special form of ordered tree encoding. To get it we first need to enumerate all nodes of a tree in level order as it is shown of the following figure.
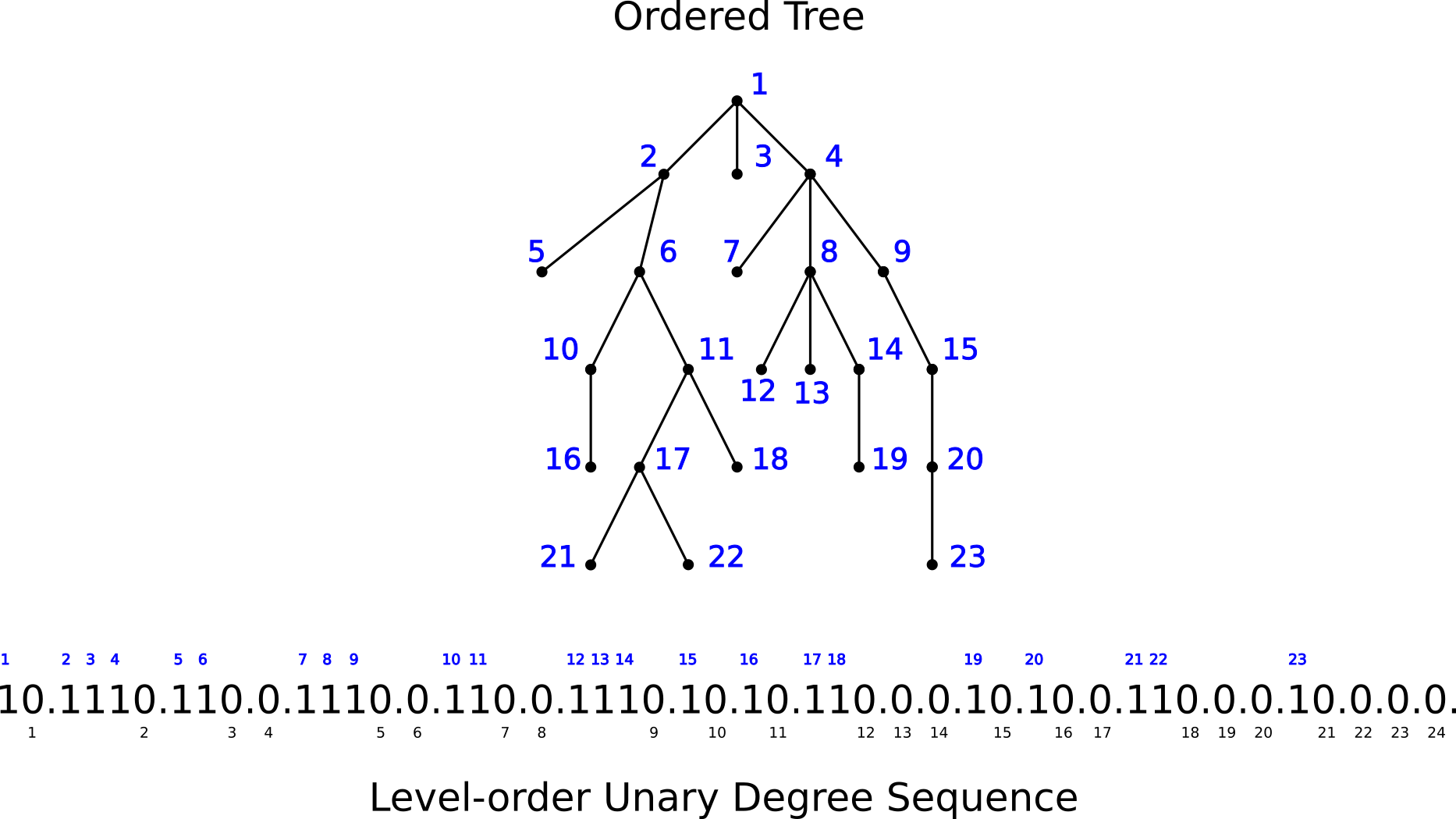
Then for each node we write its degree in unitary encoding. For example, degree of the fist node is 3, then its unitary encoding is ‘1110’. To finish LOUDS string we need to prepend substring ‘10’ to it as it is shown on the figure. Given an ordered tree on N nodes LOUDS takes no more than 2N + 1 bits. This is very succinct implicit data structure.
LOUDS is a bit vector. We also need the following operations on it:
rank1(i)– returns number of ‘1’ in the range [0, i)rank0(i)– returns number of ‘0’ in the range [0, i)select1(rnk)– returns position of rnk-th ‘1’ in the LOUDS string, rnk = 1, 2, 3, …select0(rnk)– returns position of rnk-th ‘0’ in the LOUDS string, rnk = 1, 2, 3, …
Different ways of tree node numbering for LOUDS are possible, Memoria uses the simplest one. Tree node positions are coded by ‘1’.
node_num = rank1(i + 1)– gets tree node number at positioni;i = select1(node_num)– finds position of a node in LOUDS given its number in the tree.
Having this node numbering we can define the following tree navigation operations:
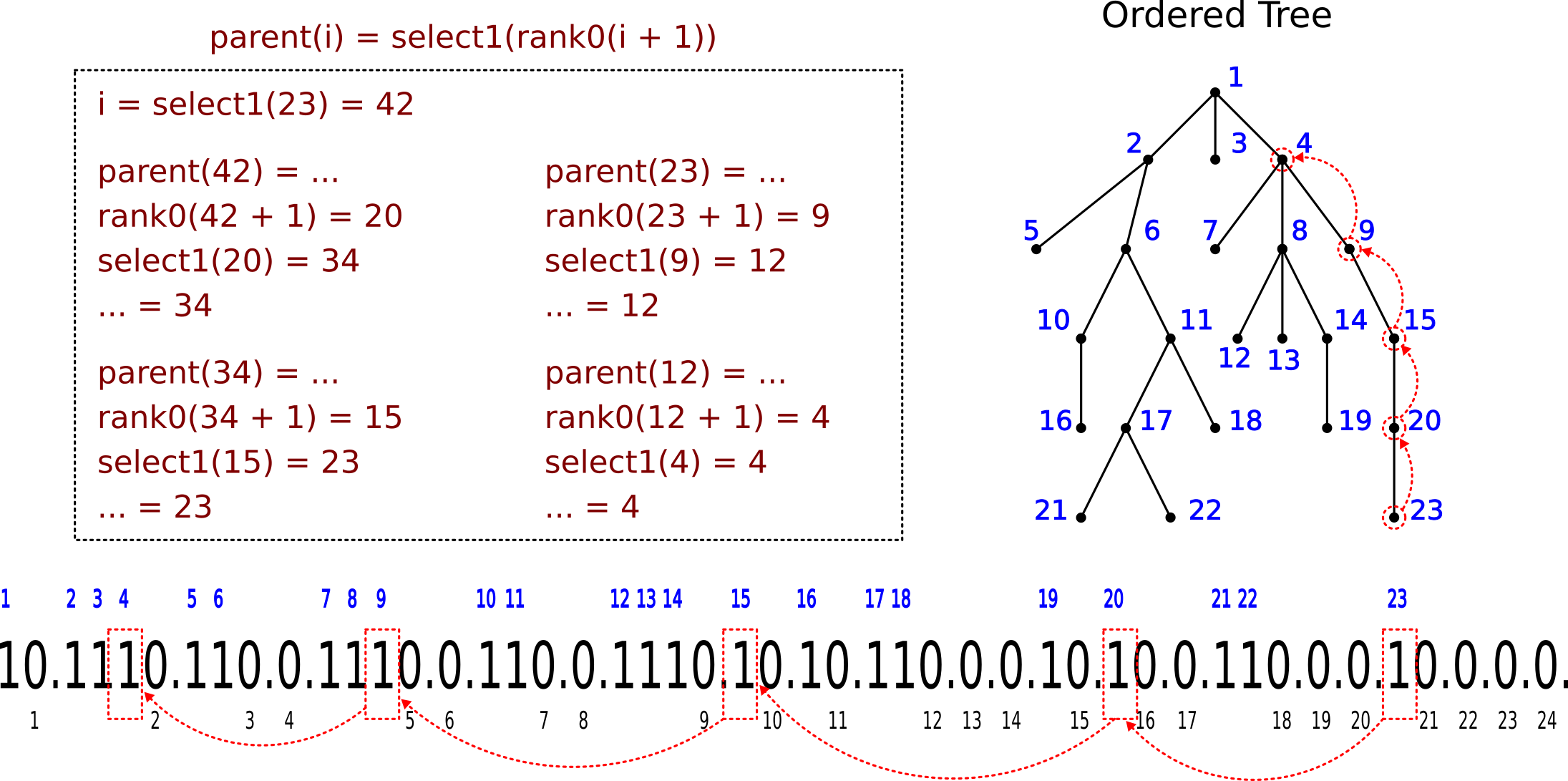
fist_child(i) = select0(rank1(i + 1)) + 1– finds position of the first child for node at the positioni;last_child(i) = select0(rank1(i + 1) + 1) - 1– finds position of the last child for node at the positioni;parent(i) = select1(rank0(i + 1))– finds position of the parent for the node at the positioni;children(i) = last_child(i) - first_child(i)– return number of children for node at the positioni;child(i, num) = first_child(i) + num– returns position of num-th child for the node at the positioni,num >= 0;is_node(i) = LOUDS[i] == 1 ? true : false– checks ifi-th position in tree node.
Note that navigation operations only defined for positions i for those is_leaf(i) == true.
Example
Let we find number of the first child for the node 8.
select1(8) = 11;first_child(11) = select0(rank1(11 + 1)) + 1 = select0(8) + 1 = 19;rank1(19 + 1) = 12.
The first child for node 8 is node 12.
The following figure shows how the parent() operation works:
Limitations
Node numbers are valid only until insertion (or deletion) into the tree. Additional data structure is necessary to keep track of node positions after tree structure updates.
Labelled Tree
Labelled tree is a LOUDS tree with a fixed set of numbers (or ‘labels’) associated with each node. It is implemented as multistream balanced tree where the first stream is dynamic bit vector with rank/select support, and the rest are streams for each label.
Streams elements distribution is very simple for this data structures. Each label belongs to a tree node that is coded by position of ‘1’ in LOUDS. Each leaf of balanced tree has some subsequence of the LOUDS.
Let we have a LOUDS sub-stream of size N with M 1s for a given leaf. Then this leaf must contain M labels in each label stream. The following expressions links together node and level positions withing a leaf:
label_idx = rank1(node_idx + 1) - 1;node_idx = select1(label_idx + 1);
Where label_idx is in [0, M) and node_idx is in [0, N)
LabeledTree uses balanced partial sum tree as a basic data structure. Because of that it optionally supports partial sums of labels is specified tree node range. The most interesting range is [0, node_idx). See Multiary Wavelet Tree for details.
Cardinal Trees
In ordered trees like in the example above, all children nodes are naturally ordered, and a node may have arbitrary number of children. In the cardinal tree of degree $D$, a node always have $D$ children, but some children can be omitted. And this information is stored in the tree, like “child $i$ is absent”. Binary search trees are cardinal trees of degree 2.
Cardinal tree of degree 4 (and greater, where degree is a power of 2) is a trie-based (or region-based) Quad Tree.
Cardinal LOUDS tree can be implemented either as a labelled tree, where node labels (from 0 to $D-1$) are cardinal labels (for sparse cardinal trees like spatial trees), or by using a searchable bitmap specifying which children are present. The bitmap can be compressed, saving space for sparse cases.
Hardware Acceleration
LOUDS trees are especially important type of compact/succinct trees, because all children of a node are stored linearly in memory, that is DRAM-friendly: traversal of a tree is a series of liner scans split by random jumps. But the number of random jumps is much smaller comparing to other types of trees. LOUDS trees do not require any specific hardware support, providing that searchable bitmap is fully accelerated.